こんにちは、小澤です。
今回は、データ分析において重要な技術である次元削減について解説していきます。次元削減とは、データの構造を整理し、より少ない情報で本質を捉えるための手法です。大量の特徴量を持つデータを効率よく扱うために欠かせない技術であり、回帰や分類といった機械学習モデルの精度向上にも大きく貢献します。また、次元削減といえば外せないのが主成分分析(PCA:Principal Component Analysis)です。
今回は、次元削減がなぜ必要なのか、どんなメリットがあるのか、そして代表的な手法であるPCAについて説明していきます。
なお、今回の内容は、教科書『Pythonによる新しいデータ分析の教科書(第2版)』の4.4.4章「次元削減」(246〜251ページ) の箇所です。
1. なぜ次元削減が必要なのか?
近年、さまざまな分野でデータの量と種類が増え続けています。たとえば、マーケティング分野では「年齢」「性別」「収入」「購買履歴」「行動ログ」などのデータが収集され、医療分野では「身長」「体重」「血圧」「血液検査結果」など、多数の測定項目が分析対象になります。
しかし、特徴量が多すぎると、以下のような問題が発生します。
- 計算コストの増大
- 過学習(オーバーフィッティング)のリスク
- 特徴量同士の冗長性
- データの可視化が難しい
こうした問題を解決するため、データの次元を減らしながら本質を保つ技術として次元削減が必要になります。
次元削減を行うことで、次のようなメリットが得られます。
- 計算が速くなる → 特徴量が減れば、学習・予測の速度が向上します。
- 過学習を抑えられる → 不要なノイズを除去し、モデルが本質的なパターンに集中できます。
- データの可視化が容易になる → 圧縮した2次元・3次元データなら、散布図などで傾向を直感的に把握できます。
- 重要な特徴を抽出できる → 予測に本当に役立つ要素だけを取り出すことができます。
2.主成分分析(PCA)
PCAは、データの持つ「分散が最大になる方向」を探し出し、そこにデータを写しなおすことで次元を圧縮する手法です。イメージとしては、ばらばらに広がったデータを、できるだけ情報量を失わずに、少ない軸にまとめる作業だと考えるとよいでしょう。
ここでは、scikit-learnを使って糖尿病データセットに対してPCAを実施してみましょう。なお、この糖尿病データセットは、糖尿病患者の疾患進行度(病気の重さ)を予測することを目的として構成されており、以下のような特徴を持ちます。
- サンプル数: 442件(患者ごとのデータ)
- 特徴量: 10個の定量的な身体的測定項目(すべて標準化済み)
- 目的変数: 1年後の病気の進行度を表す定量スコア(連続値)
1)データの準備と標準化
まず、糖尿病データセットを読み込み、標準化(平均0、分散1)を行います。
from sklearn.datasets import load_diabetes
from sklearn.preprocessing import StandardScaler
# データの読み込み
data = load_diabetes()
X = data.data
# 特徴量の標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)2)PCAの実行
2つの主成分に次元を圧縮してみます。
from sklearn.decomposition import PCA
# PCAの実行(2次元に圧縮)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
print(X_pca.shape) # → (442, 2)これで、もともと10個あった特徴量が2つに圧縮されます。
3)主成分の寄与率を確認
各主成分がどれくらい情報を保持しているかを確認できます。
print(pca.explained_variance_ratio_) # → [0.40242108 0.14923197]
print("累積寄与率:", sum(pca.explained_variance_ratio_)) # → 累積寄与率: 0.5516530427751478ここで得られる累積寄与率が高ければ、高いほど、元データの情報をしっかり保っていることを意味します。ここでは、上位2つの主成分だけで約55%の情報を保持していることがわかります。
4)PCA後のデータを可視化
圧縮した2次元データを散布図にして、データの構造を視覚的に確認しましょう。
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
plt.scatter(X_pca[:, 0], X_pca[:, 1], alpha=0.7)
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.title("PCA of Diabetes Dataset")
plt.grid(True)
plt.show()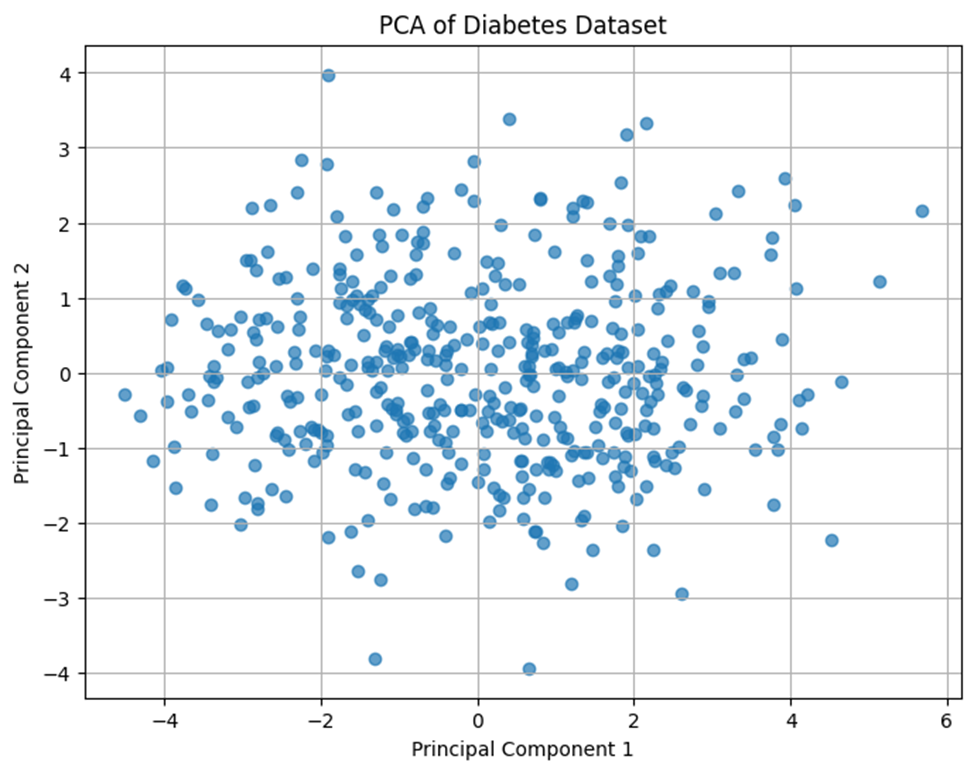
この散布図から、糖尿病データの大まかな分布傾向が2軸だけでかなり把握できることがわかります。
3. PCAは実際にどう役立つか?
たとえば、次元削減後のデータで回帰モデルを再構築すると、以下のような効果が期待できます。
- 特徴量が少ない分、学習が速くなる
- モデルがシンプルになり、過学習のリスクが減る
- 解釈しやすいモデルになる
また、視覚化を通じて、データ同士の関係性やクラスの傾向を直感的に把握できるのも大きなメリットです。
4. まとめ
次元削減は、データを整理して効率よく扱うために不可欠な技術です。特に、特徴量が多いデータに対しては、次元削減により計算コストや過学習リスクを抑えることができます。中でも主成分分析(PCA)は、最も代表的な次元削減手法です。実際にPCAを使用することで、情報の損失を最小限に抑えつつ、特徴量を減らすことが可能です。データの見通しが良くなり、モデルの精度向上や可視化にも大きな効果を発揮できるでしょう。
次回は「モデルの評価」や「クラスタリング」について解説を進めていきましょう。モデルの評価では、混同行列・正解率・F1スコアなどの指標、クラスタリングではK-meansや階層型クラスタリングなどを取り上げます。ぜひ次回もお楽しみに。
