こんにちは、小澤です。
今回は、機械学習で基本として取り上げられる「回帰(Regression)」について解説していきます。回帰は連続的な数値を予測するための手法で、分類と並び、あらゆる分野で広く使われています。特に、数値予測を行う基本技術として、機械学習の中でも最も実用的な手法といえます。
なお、今回の内容は、教科書『Pythonによる新しいデータ分析の教科書(第2版)』の4.4.3章「回帰」(244〜246ページ) の箇所です。
1. 回帰とは?
回帰は、入力された数値データに基づいて、連続的な数値を予測するためのモデルです。たとえば、以下のような場面で使われます。
- 家の面積や築年数から住宅価格を予測する
- BMIや年齢から病気の進行度を予測する
- 広告費や販促データから売上を予測する
- 過去の気象データから翌日の気温を予測する
回帰は「数値を予測」するため、連続値(例えば100.3や42.7など)を返すのが特徴です。
機械学習や統計、回帰分析などの分野でよく登場する用語に、「説明変数」と「目的変数」があります。これらは、入力と出力の役割を表します。
1)説明変数
- モデルに入力として与えるデータ
- 予測や分析の「もとになる情報」
- 何をもとにして結果を予測するか? にあたる部分です。
- 例えば、
- 家賃を予測したい → 「部屋の広さ」「築年数」「駅からの距離」など
- 病気の進行度を予測したい → 「年齢」「BMI」「血圧」など
2)目的変数
- モデルが予測・説明しようとする対象
- 説明変数に対して「結果として得られる値」
- 何を予測・説明したいのか? にあたる部分です。
- 例えば、
- 家賃を予測したい → 「家賃の金額」
- 病気の進行度を予測したい → 「病気の進行度スコア」
Pythonのコードなどでは、一般的に以下のように変数を割り当てます。
X = 説明変数(入力)
y = 目的変数(出力)
2. 線形回帰
線形回帰は、「入力と出力の関係を、まっすぐな線(直線や平面)で表現して予測する方法」です。入力が増えると出力も増える、あるいは減る、というようなシンプルな関係性をモデル化したいときに使われます。
例えば、
- 広い部屋ほど家賃が高くなる
- 年齢が上がると健康リスクも高くなる
といったような、「Aが大きくなるとBも大きくなる(または小さくなる)」という関係を、直線的に捉えるのが線形回帰です。
1)単回帰
単回帰は、線形回帰の中でも入力(説明変数)が1つだけのシンプルなケースです。
- 部屋の広さから家賃を予測する
- 人の身長から体重を予測する
グラフにすると散布図の中に直線を1本引くことで、予測モデルを表すことができます。視覚的にも直感的にもわかりやすいため、学習の初期段階やシンプルな予測に適しています。
2)重回帰
重回帰は、入力(説明変数)が2つ以上ある線形回帰です。つまり、複数の要素を使って、1つの結果を予測するモデルです。
- 「部屋の広さ」と「駅からの距離」と「築年数」の3つを使って家賃を予測する
- 「年齢」「BMI」「血圧」の3つを使って病気の進行度を予測する
複数の要素を組み合わせて結果を説明しようとするのが重回帰です。単回帰よりも現実の問題に近く、実務で多く使われます。
3. 糖尿病データセットを用いた回帰
scikit-learnに内蔵された「糖尿病(Diabetes)データセット」を用いて、患者の身体情報から病気の進行度(数値)を予測するモデルを構築し、回帰モデルによって病気の進行度を予測する一連の流れを説明します。
回帰分析は基本的に以下のようなステップで進めます。
- データの読み込みと前処理
- データの分割(学習用とテスト用)
- モデルの構築と訓練(fit)
- 予測(predict)
- モデルの性能評価
- 予測結果の可視化
- 必要に応じて改善・再学習
1.データの読み込みと前処理
まずはデータを読み込み、モデルに適した形式へと整えます。
from sklearn.datasets import load_diabetes
from sklearn.preprocessing import StandardScaler
# データの読み込み
data = load_diabetes()
X = data.data # 特徴量(10個の数値)
y = data.target # 予測対象(病気の進行度)
# 特徴量を標準化(平均0、分散1)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
- 特徴量のスケーリング(標準化)は、線形回帰などのアルゴリズムで性能向上に役立つことが多いです。
- 糖尿病データセットには、年齢やBMI、血圧などの身体指標が含まれています。
2.データの分割(学習用とテスト用)
モデルの学習と評価を分けるために、データを学習用とテスト用に分割します。 学習データだけで評価してしまうと、過学習に気づけず、実用性のないモデルになる恐れがあります。モデルは、学習データを何度も見て最適化されます。すると、学習データにはよく当てはまるが、新しいデータには弱いという状態(過学習)になってしまうことがあります。これを防ぐために、訓練に使わないデータを別に用意し、モデルの「汎化性能(未知のデータにも強いか)」を確かめます。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
- train_test_split によって、データの80%を学習用、20%をテスト用に分けています。
- テストデータは「未知のデータ」として扱い、モデルの性能評価に使います。
3.モデルの構築と訓練(fit)
次に、線形回帰モデルを構築し、学習データを使って訓練します。
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
- fit() は「モデルが入力と出力の関係を学習する」ステップです。
- 線形回帰では、10個の特徴量に対して最適な重み(係数)と切片を学習します。
4.予測(predict)
学習が完了したら、テスト用データを使って予測を行います。
y_pred = model.predict(X_test)
print(y_pred)

- predict() によって、未知の入力に対して病気の進行度を予測できます。
- 出力は連続値で、分類とは異なることがわかります。
5.モデルの性能評価
予測結果がどれくらい正しいのか、数値で評価します。
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
mse = mean_squared_error(y_test, y_pred) # 平均二乗誤差
mae = mean_absolute_error(y_test, y_pred) # 平均絶対誤差
r2 = r2_score(y_test, y_pred) # 決定係数
print(mse)
print(mae)
print(r2)
- 「平均二乗誤差(MSE: Mean Squared Error)」は、予測値と実測値の誤差を二乗して平均した値で、値が小さいほど誤差が少なく、精度が高いことを示します。二乗することで大きな誤差により強く反応する特徴があり、外れ値の影響を受けやすいという側面もあります。
- 「平均絶対誤差(MAE: Mean Absolute Error)」は、予測と実測の差の絶対値を平均したもので、MSEよりも外れ値に強く、より直感的に誤差の大きさを把握しやすい指標です。
- 「決定係数(R²スコア)」は、モデルがどの程度データの変動を説明できているかを表す指標です。1に近いほどモデルの説明力が高く、予測がうまくできていることを意味します。逆に、0に近づくほど「何も説明できていない」状態を示します。
6.予測結果の可視化
実測値と予測値の関係を散布図で可視化すると、モデルの傾向がつかみやすくなります。
import matplotlib.pyplot as plt
plt.scatter(y_test, y_pred, alpha=0.7)
plt.xlabel("Actual")
plt.ylabel("Predicted")
plt.title("Actual vs Predicted Diabetes Progression")
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--')
plt.grid(True)
plt.show()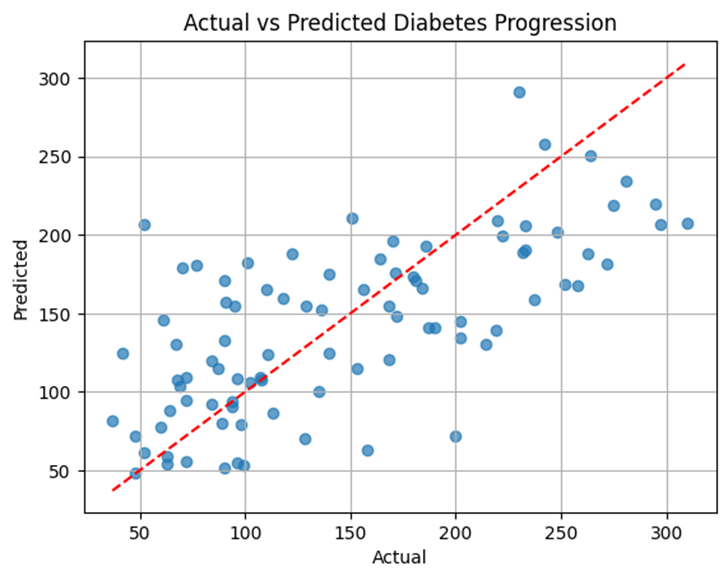
- 点が赤い直線(理想的な予測)に近いほど、良い予測ができていると言えます。
- 散布図を使うと、偏りや外れ値の傾向も見えてきます。
7.必要に応じて改善・再学習
モデルの精度が不十分だと感じた場合は、以下のような対策を考えます。
- 特徴量の見直し…不要な特徴を除いたり、重要な特徴を追加したりする
- 他の回帰手法の導入…リッジ回帰、ラッソ回帰、決定木回帰などを試す
- 前処理の改善…標準化や外れ値処理、変数のスケーリングなど
- ハイパーパラメータの調整 …モデルの内部設定を変更して性能を最適化する
4. リッジ回帰とラッソ回帰
線形回帰はシンプルですが、多くの特徴量がある場合や、相関のある特徴量が存在する場合には過学習を起こしやすいという弱点があります。このとき活用されるのが、以下の 正則化つき回帰モデル です。
1.リッジ回帰(Ridge Regression)
- 重みの大きさにペナルティ(L2ノルム)をかける
- モデル全体のバランスを保ちながら学習
2.ラッソ回帰(Lasso Regression)
- 重みの絶対値にペナルティ(L1ノルム)をかける
- 不要な特徴量の重みをゼロにし、自動で特徴量選択も行える
リッジ回帰やラッソ回帰は、精度は線形回帰と大差ないですが、過学習のリスクが低く、より安定的です。特に、ラッソ回帰は特徴量選択の効果もあるため、解釈性が求められる場面に適しています。大規模データやノイズの多いデータでは、リッジ・ラッソの効果がさらに明確になります。
5. まとめ
回帰は、連続的な数値を予測するための基本的かつ実用的な手法です。scikit-learnを使えば、データの前処理からモデルの構築、評価、可視化までを効率的に行うことができます。
次回は、次元削減について説明します。次元削減は、データの構造を整理し、より少ない情報で本質をとらえる手法です。回帰と組み合わせて分析精度を高める方法や、代表的な手法である主成分分析(PCA)についても取り上げる予定です。ぜひ次回もお楽しみに。
