こんにちは、小澤です。
これまでに見てきた「分類」や「回帰」は、あらかじめ正解ラベルが与えられているデータを用いて学習を行う「教師あり学習」に分類されるものでした。一方で、「教師なし学習」は、正解ラベルのないデータからパターンや構造を見つけ出す手法を指します。
その中でも特に代表的な手法がクラスタリングです。クラスタリングでは、データの類似性や距離関係に基づいて、自然なグループ(クラスタ)に分けることを目的とします。クラスタリングの結果は「分類」と似たような形になりますが、あらかじめ定義された正解ラベルを必要としないという点で本質的に異なります。
クラスタリングでは、与えられたデータを「似た者同士」にまとめてグループ化します。代表的な用途として、以下のようなさまざまな分野で活用されています。
- マーケティング:顧客を購買パターンや嗜好に応じてグループ分けする(セグメンテーション)
- 画像処理:似たような色や形のピクセルをまとめて物体を抽出
- 異常検知:通常と異なるグループに属するデータを検出
- 文書分析:似たトピックを含む文書を自動的に分類する
教師なし学習であるため、「何が正解か」を明示的に定義できない状況でも、データ構造の理解や予備分析に役立ちます。
今回の内容は、教科書『Pythonによる新しいデータ分析の教科書(第2版)』の4.4.7章「クラスタリング」(264〜270ページ) の箇所です。
1. k-meansクラスタリング
k-means(ケイ・ミーンズ)法は、最も広く使われているクラスタリング手法のひとつです。以下のような手順で進行します。
- クラスタ数 K をあらかじめ指定
- ランダムに K 個のクラスタ中心(セントロイド)を初期化
- 各データ点を、最も近い中心点に割り当てる(ユークリッド距離など)
- 割り当てられたデータの平均を新しいクラスタ中心とする
- クラスタの割り当てが収束するまで繰り返す
このアルゴリズムはシンプルで計算コストも低いため、多くのシナリオで用いられています。
例えば、以下は、アヤメ(iris)データセットのうち、2つの特徴量をもとにk-meansクラスタリングを行うサンプルコードです。ここで使われている特徴量は、「Sepal length(がく片の長さ)」と「Sepal width(がく片の幅)」です。
| from sklearn.datasets import load_iris from sklearn.cluster import KMeans import matplotlib.pyplot as plt # データの読み込み(irisデータ) iris = load_iris() X = iris.data[:, :2] # 最初の2つの特徴量だけ使用 # k-meansクラスタリング(クラスタ数=3) kmeans = KMeans(n_clusters=3, random_state=42) kmeans.fit(X) labels = kmeans.labels_ # 結果の可視化 plt.scatter(X[:, 0], X[:, 1], c=labels, cmap=’viridis’, edgecolor=’k’) plt.xlabel(“Sepal length”) # がくの長さ plt.ylabel(“Sepal width”) # がくの幅 plt.title(“K-means Clustering”) plt.show() |
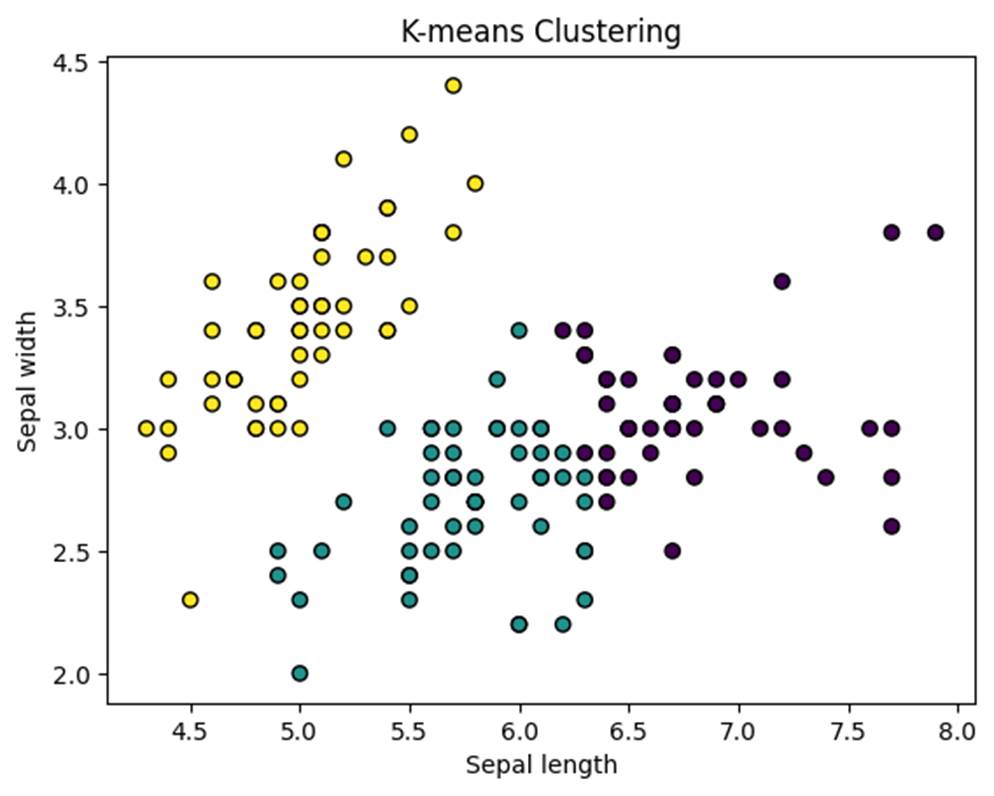
教師なしでデータが自然に3つのグループに分けられる様子が確認できます。
- k-meansは教師なし学習の手法なので、ラベル(花の種類など)は使われていません。
- kmeans.fit(X) によって、2つの特徴量だけに基づいて、データを3つのグループ(クラスタ)に分けています。
- labels = kmeans.labels_ により、各データ点がどのクラスタに属するかが決定されます。
- グラフの描画では、c=labels によってクラスタごとに色分けされています。
注意点は以下です。
- k を事前に決める必要があります。つまり、適切なクラスタ数の選択が課題です。
- 初期化の仕方によって結果が変わる可能性があります。
- 球状クラスタや同じサイズ・密度のクラスタでないと精度が落ちやすくなります。
2. 階層型クラスタリング
階層型クラスタリングは、クラスタの入れ子構造を考慮する手法です。主に2つの方式があります。
- 凝集型(下位から上位へ、ボトムアップ)
- 分割型(上位から下位へ、トップダウン)
凝集型が一般的で、以下のように処理を進めます。
- 各データ点を1つのクラスタとみなす(初期状態)
- 距離が最も近い2つのクラスタを結合
- 全体が1つになるまで繰り返す
また、クラスタ間の距離をどう定義するかで、結果が大きく異なります。
- 単連結法(最短距離)
- 完全連結法(最長距離)
- 平均連結法(平均距離)
- ウォード法(クラスタ内の分散が最小になるよう結合)
以下は、アヤメ(iris)データセットの2つの特徴量を使って階層型クラスタリングを実行して、その結果をデンドログラムで視覚化するサンプルコードです。デンドログラムを使うことで、データのクラスタ構造をツリー状に視覚化でき、どの部分で分ければ適切かを直感的に判断できます。
| from sklearn.datasets import load_iris from scipy.cluster.hierarchy import dendrogram, linkage import matplotlib.pyplot as plt X = load_iris().data[:, :2] linked = linkage(X, method=’ward’) # デンドログラムの描画 plt.figure(figsize=(10, 6)) dendrogram(linked, orientation=’top’, distance_sort=’descending’, show_leaf_counts=False) plt.title(“Hierarchical Clustering Dendrogram”) plt.xlabel(“Sample index”) plt.ylabel(“Distance”) plt.show() |

このグラフは、
- 横軸(Sample index):データのインデックス(並び順)
- 縦軸(Distance):クラスタ間の結合距離(類似度の逆)
つまり、枝が高い場所で結合されているほど、似ていないクラスタ同士だったことを示しています。
階層型クラスタリングの特徴は以下です。
- クラスタ数を事後的に決められるので、柔軟性が高い。
- 距離や結合法によって表現力が変化する。
- 計算量は多めだが、小規模データには有効。
3.まとめ
クラスタリングは、教師なし学習の基本的な手法のひとつです。データの分類や可視化、前処理、異常検知など幅広く利用されています。k-meansはシンプルで高速な手法として、多くの実務に適しています。一方、階層型クラスタリングは柔軟な構造理解に役立ち、デンドログラムを使えば直感的な分析も可能です。クラスタリングを活用することで、ラベルがないデータの「隠れた構造」を明らかにできるので、分類や回帰の前段階としても役立てることができます。
次回は、これまで使ってきた scikit-learn 以外の機械学習ライブラリについて紹介します。より高性能なモデルや、大規模なデータに対応するためのツールもいろいろありますので、それぞれの特徴や使いどころを解説したいと思います。ぜひ次回もお楽しみに。
